시간복잡도(Time Complexity)
>개요
: 문제를 해결하며 중요한 것은 답과 효율이다.
: 답을 찾는 것은 알고리즘에 대한 이해와 능력이 필요
: 효율적인 측면은 시간복잡도에 대한 이해와 능력이 필요
>의미
: '입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?' 를 의미
: 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화하는 것이 효율적인 알고리즘이다!
>시간 복잡도 표기법
- Big-O(빅-오)
: 최악을 고려하는 표기법
: ~정도 시간까지 걸릴 수 있다.
- Big-Ω(빅-오메가)
: 최선을 고려하는 표기법
: 최소 ~정도 시간이 걸린다
- Big-θ(빅-세타)
: 평균을 고려하는 표기법
: 평균적으로 ~정도 시간이 걸린다.
=>Big-O 표기법의 표현이 문제가 발생한 상황에 적절한 대응을 하기 쉽기 때문에 Big-O 표기법을 주로 사용한다.
Big-O 표기법
>함수와 비교
function : y = a*x
O(log n)
O : Big-O 표기 (function)
( ) : 입력값에 따른 시간 변화 (n을 대입한 y)
n : 입력값(x)
>Big-O Chart


>O(1)
: constant complexity
: 입력값이 증가하더라도 걸리는 시간은 그대로 유지
: 입력값 크기와 관계없이, 즉시 출력값을 얻을 수 있음.
public static void constantComplexity(int n){
System.out.println(n);
}

>O(n)
: linear complexity
: 입력값에 비례하여 걸리는 시간이 증가
: 반복문의 경우가 이에 해당한다.
: O(n)의 코드가 5개 있다고 해서 O(5n)이 아닌 O(n)으로 표현함.
: 입력값의 크기가 커지면 코드의 갯수는 큰 의미가 없어지기 때문
public static void linearComplexity(int n){
for (int i = 0; i < n; i++) {
System.out.println(n);
}
}
>O(log n)
: logarithmic complexity
: O(1) 다음으로 빠른 시간 복잡도
: 곱하기나 나누기로 특정 정수만큼 뚝뚝 변하는 코드들이 logarithmic complexity이다.
: 일반적인 예시로는 이진 검색 알고리즘이 있다.
public static void logarithmicComplexity(int n){
for (int i = 0; i < n; i*=2) {
System.out.println(n);
}
}
>O(n^2)
: quadratic complexity
: 이중 반복문인 경우 이에 해당한다.
public static void quadraticComplexity(int n){
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.println(n);
}
}
}
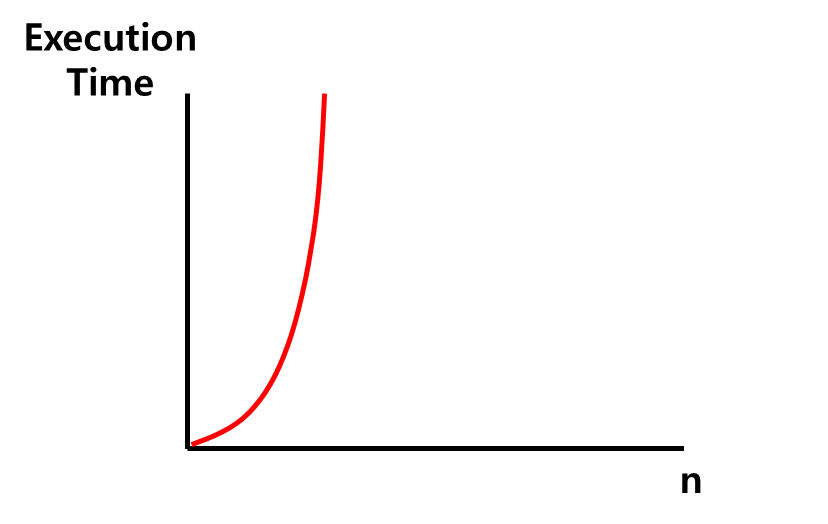
>O(2^n)
: exponential complexity
: 재귀로 구현한 피보나치 수열이 대표적인 예시
public int fibonacci(int n) {
if(n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci (n - 2);
}
//코드가 빠른 순으로 정리한 표
참고: https://scshim.tistory.com/257
//컬렉션들의 시간복잡도 정리 표
참고: https://hbase.tistory.com/185
//시간 복잡도 예시 문제
참고: https://dingrr.com/blog/post/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EC%8B%9C%EA%B0%84%EB%B3%B5%EC%9E%A1%EB%8F%84-%EC%98%88%EC%A0%9C-15%EC%A2%85
>데이터(입력값) 크기 제한에 따른 시간 복잡도 예측
: 문제에서 주어진 데이터의 크기를 보고 어떤 종류의 시간 복잡도 내로 풀 수 있을지 예측할 수 있음.
<예시 표 정리>
참고 링크: https://qlalzl9.tistory.com/176
'코드스테이츠_국비교육 > [Section2]' 카테고리의 다른 글
| 26.04_완전 탐색 알고리즘_22.09.27 (0) | 2022.09.28 |
|---|---|
| 26.03_탐욕 알고리즘_22.09.27 (0) | 2022.09.27 |
| 26.01_코딩 테스트 준비_22.09.27 (0) | 2022.09.27 |
| 25_Searching Algorithm_22.09.26 (0) | 2022.09.26 |
| 24.03_Binary Search Tree_22.09.23 (0) | 2022.09.25 |